3.3.1. 關聯度
實作一個每個快取行都能保存任意記憶體位置副本的快取是有可能的(見圖 3.5)。這被稱為一個全關聯式快取(fully associative cache)。要存取一個快取行,處理器核心必須要將每個快取行的標籤與請求位址的標籤進行比較。標籤會由位址中不是快取行偏移量的整個部分組成(這表示在 3.2 節圖示中的 為零)。
有些快取是像這樣實作的,但是看看現今使用的 L2 數量,證明這是不切實際的。給定一個有著 64B 快取行的 4MB 快取,這個快取將會有 65,536 個項目。為了達到足夠的效能,快取邏輯必須要能夠在短短幾個週期內,從這所有的項目中挑出符合給定標籤的那一個。實作這點要付出龐大的精力。
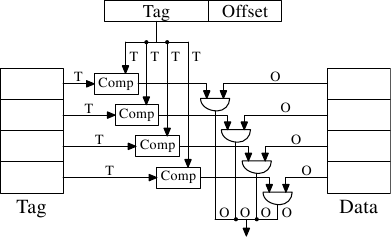
對每個快取行來說,都需要一個比較器(comparator)來比對很大的標籤(注意, 為零)。緊鄰著每條連線的字母代表以位元為單位的寬度。假如沒有給定,那麼它就是一條單一位元的線路。每個比較器都必須比對兩個 位元寬的值。接著,基於這個結果,選擇合適的快取行內容,並令它能被取得。有多少快取行,都得合併多少組 資料線。實作一個比較器所需的電晶體數量很大,特別是它必須運作地非常快的時候。疊代比較器(iterative comparator)是不可用的。節省比較器數量的唯一方式,就是反覆地比較標籤以減少比較器的數量。這與疊代比較器並不合適的理由相同:它太花時間了。
全關聯式快取對小快取(例如在某些 Intel 處理器的 TLB 快取就是全關聯式的)來說是有實用價值的,但那些快取都很小,非常小。我們所指的是至多只有幾十個項目的情況。
對 L1i、L1d、以及更高層級的快取來說,需要採用不同的方法。我們所能做的是限縮搜尋。在最極端的限制中,每個標籤都恰好對映到一個快取項目。計算方式很簡單:給定 4MB/64B、有著 65,536 個項目的快取,我們能夠直接使用位址的 6 到 21 位元(16 個位元)來直接定址每個項目。低 6 位元是快取行內部的索引。
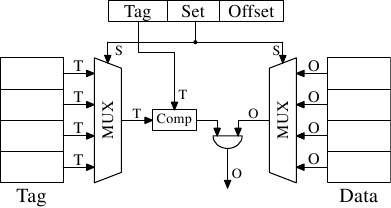
如圖 3.6 所見到的,這種直接對映式快取(direct-mapped cache)很快,而且實作起來相對簡單。它需要一個比較器、一個多工器(在這張示意圖中有兩個,標籤與資料是分離的,但在這個設計上,這點並不是個硬性要求)、以及一些用以選擇有效快取行內容的邏輯。比較器是因速度要求而複雜,但現在只有一個;因此,便能夠花費更多的精力來讓它變快。在這個方法中,實際的複雜之處都落在多工器上。在一個簡易的多工器上,電晶體的數量以 成長,其中 為快取行的數量。這能夠容忍,但可能會慢了點,在這種情況下,藉由在多工器中增加更多的電晶體以平行化某些工作,便能夠提升速度。電晶體的總數能夠緩慢地隨著快取大小的成長而成長,使得這種解法非常有吸引力。但它有個缺點:只有在程式用到的位址,對於用以直接映射的位元來說是均勻分佈的情況下,它才能運作得很好。若非如此,而且經常這樣的話,某些快取項目會因為頻繁地使用而被重複地逐出,而其餘的項目則幾乎完全沒用到、或者一直是空的。
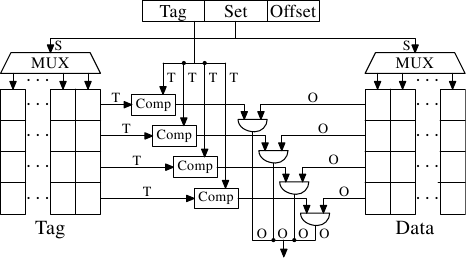
這個問題能藉由讓快取集合關聯(set associative)來解決。一個集合關聯式快取結合了全關聯式以及直接對映式快取的良好特質,以在很大程度上避免了那些設計的弱點。圖 3.7 顯示了一個集合關聯式快取的設計。標籤與資料的儲存被分成集合,其中之一會被快取行的位址所選擇。這與直接對映式快取相似。但少數的值能以相同的集合編號快取,而非令快取中的每個集合編號都只有一個元素。所有集合內成員的標籤會平行地比對,這與全關聯式快取的運作方式相似。
結果是,快取不容易被不幸地––或者蓄意地––以相同集合編號的位址選擇所擊敗,同時快取的大小也不會受限於能被經濟地實作的比較器的數量。假如快取增長,它(在這張圖中)只有行數會增加,列數則否。行數(以及比較器)只會在快取的關聯度(associativity)增加的時候才會增加。現今的處理器為 L2 或者更高層級的快取所使用的關聯度層級高達 24。L1 快取通常使用 8 個集合。
給定我們的 4MB/64B 快取以及 8 路(8-way)集合關聯度,於是這個快取便擁有 8,192 個集合,並且僅有 13 位元的標籤被用於定址快取集。要決定快取集中的哪個(如果有的話)項目包含被定址的快取行,必須要比較 8 個標籤。在非常短的時間內做到如此是可行的。藉由實驗我們能夠看到,這是合理的。
| L2 快取大小 | 關聯度 | |||||||
|---|---|---|---|---|---|---|---|---|
| 直接 | 2 | 4 | 8 | |||||
| CL=32 | CL=64 | CL=32 | CL=64 | CL=32 | CL=64 | CL=32 | CL=64 | |
| 512k | 27,794,595 | 20,422,527 | 25,222,611 | 18,303,581 | 24,096,510 | 17,356,121 | 23,666,929 | 17,029,334 |
| 1M | 19,007,315 | 13,903,854 | 16,566,738 | 12,127,174 | 15,537,500 | 11,436,705 | 15,162,895 | 11,233,896 |
| 2M | 12,230,962 | 8,801,403 | 9,081,881 | 6,491,011 | 7,878,601 | 5,675,181 | 7,391,389 | 5,382,064 |
| 4M | 7,749,986 | 5,427,836 | 4,736,187 | 3,159,507 | 3,788,122 | 2,418,898 | 3,430,713 | 2,125,103 |
| 8M | 4,731,904 | 3,209,693 | 2,690,498 | 1,602,957 | 2,207,655 | 1,228,190 | 2,111,075 | 1,155,847 |
| 16M | 2,620,587 | 1,528,592 | 1,958,293 | 1,089,580 | 1,704,878 | 883,530 | 1,671,541 | 862,324 |
表 3.1 顯示了對於一支程式(在這個例子中是 gcc,根據 Linux 系統核心的人們的說法,它是所有基準中最重要的一個)在改變快取大小、快取行大小、以及關聯度集合大小時,L2 快取錯失的次數。在 7.2 節中,我們將會介紹對於這個測試,所需要用以模擬快取的工具。
以防這些值的關聯仍不明顯,這所有的值的關係是,快取的大小為
位址是以 3.2 節的圖中示意的方式,使用
來對映到快取中的。
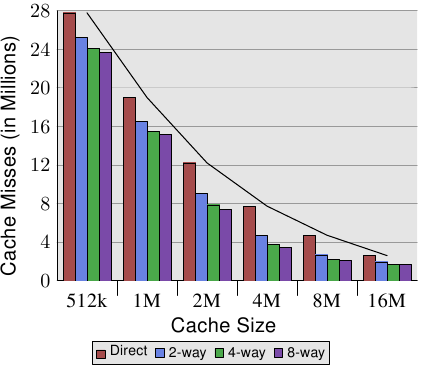
圖 3.8 讓這個表格的數據更容易理解。它顯示了快取行大小固定為 32 位元組的數據。看看對於給定快取大小的數字,我們可以發現關聯度確實有助於顯著地降低快取錯失的次數。以一個 8MB 快取來說,從直接對映式變成 2 路集合關聯式避免了幾乎 44% 的快取錯失。相比於一個直接對應式快取,使用一個集合關聯式快取的話,處理器能夠在快取中保存更多的工作集。
在文獻中,偶爾會讀到引入關聯度與加倍快取大小有著相同的影響。在某些極端的例子中,如同能夠從 4MB 跳到 8MB 快取所看到的,確實如此。但再一次加倍關聯度的話,顯然就不是如此了。如同我們能從數據中所看到的,接下來的提升要小得多。不過,我們不該完全低估這個影響。在範例程式中,記憶體使用的尖峰為 5.6M。所以使用一個 8MB 快取,同樣的快取集不大可能被多次(超過兩次)使用。有個較大的工作集的話,能夠節約的更多。如同我們能夠看到的,對於較小的快取大小來說,關聯度的獲益較大。
一般來說,將一個快取的關聯度提升到 8 以上,似乎對一個單執行緒的工作量來說只有很小的影響。隨著共享第一層快取的超執行緒處理器、以及使用一個共享 L2 快取的多核心處理器的引入,形勢轉變了。現在你基本上會有兩支程式命中相同的快取,這導致關聯度會在實務上打對折(對四核處理器來說是四分之一)。所以能夠預期,提升核心的數量,共享快取的關聯度也應該成長。一旦這不再可能(16 路集合關聯度已經很難了),處理器設計師就必須開始使用共享的 L3 或者更高層級的快取,而 L2 快取則是潛在地由核心的子集所共享。
我們能在圖 3.8 學到的另一個影響是,增加快取大小是如何提升效能的。這個數據無法在不知道工作集大小的情況下解釋。顯然地,一個與主記憶體一樣大的快取,會導致比一個較小快取更好的結果,所以一般來說不會有帶著可預見優勢的最大快取大小的限制。
如同上面所提到的,工作集大小的尖峰為 5.6M。這並沒有給我們任何最佳快取大小的確切數字,但它能讓我們估算出這個數字。問題是,並非所有被用到的記憶體都是連續的,因此我們會有––即使是以一個 16M 的快取與一個 5.6M 的工作集––衝突(conflict)譯註(看看 2 路集合關聯式的 16MB 快取相較於直接對映版本的優勢)。但有把握的是,以同樣的工作量,一個 32MB 快取的獲益是可以忽略不計的。但誰說過工作集大小必須維持不變了?工作量是隨著時間成長的,快取大小也應該如此。在購買機器、並且在你得去挑選願意為此買單的快取大小時,是值得去衡量工作集大小的。在圖 3.10 中能夠看到這件事何以重要。
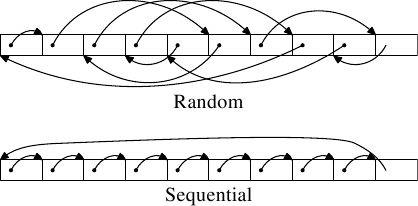
執行了兩種類型的測試。在第一個測試中,元素是循序處理的。測試程式沿著指標(pointer)n 前進,但陣列元素會以令它們以在記憶體中排列的順序被巡訪的方式鏈結。這能夠在圖 3.9 的下半部看到。有個來自最後一個元素的回溯參考。在第二個測試中(圖中的上半部),陣列元素是以隨機順序巡訪的。在這兩種情況中,陣列元素都會形成一個循環的單向鏈結串列(single-linked list)。
譯註. 這裡指的是上文描述直接對映式快取時所提到的缺點。 ↩